实战篇-php之apc

centos

1
2
3
4
5
6
7
8
9
10
11
12
13
14
yum install php-devel.x86_64
#yum install gcc automake php httpd httpd-devel
yum install php-pear
yum install php-devel.x86_64
yum install pcre-devel
yum install nginx
yum install php-fpm.x86_64
yum install mysql-server.x86_64
yum install git
yum install php-mysql.x86_64
pecl install apc
echo "extension=apc.so" >> /etc/php.ini
echo "apc.enabled=1" >> /etc/php.ini

展开全文 >>

实战篇-nginx和php-fpm环境搭建

centos

安装服务
1
2
yum install nginx
yum install php-fpm
配置服务
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
mv /etc/nginx/conf.d/default.conf /etc/nginx/conf.d/xxx.conf
将xxx.conf文件内容修改为如下:
server {
    listen       80 default_server;
    root         path/to/home;
    index index.php;
    location ~ \.php$ {
        fastcgi_pass 127.0.0.1:9000;
        fastcgi_index index.php;
        fastcgi_param SCRIPT_FILENAME $document_root$fastcgi_script_name;
        include fastcgi_params;
    }
    error_page 404 /404.html;
        location = /40x.html {
    }
    error_page 500 502 503 504 /50x.html;
        location = /50x.html {
    }
}

在path/to/home目录下新建index.php文件

1
2
3
<?php
    echo "hello world";
?>
启动服务
1
2
service php-fpm start
service nginx start

展开全文 >>

理论篇-LRU

LRU(Least recently used)，最近最少被使用。该算法根据历史访问记录淘汰缓存数据，其理论依据是最近很少被使用的，以后使用的概率也不会太大。

最简单的LRU

实现:底层数据结构采用单链表。查询时，首先检查缓存是否命中，若命中，则将命中的元素插入到链表的头，若未命中，则从原始存储中查找数据，然后将数据插入到链表的头。在将新元素插入到链表的头部时，若此时空间已满，则淘汰末尾的元素。

lru_1

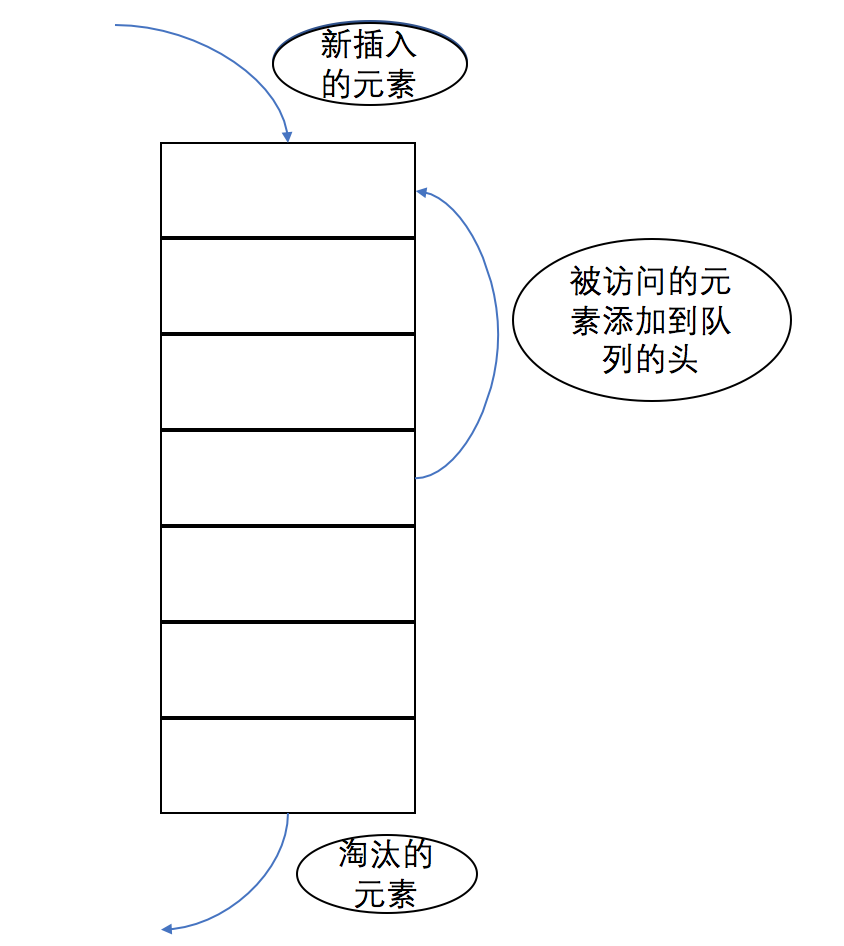
点评:实现简单，对于热点数据的访问，效果很好，但对于周期性的数据访问，效果很差

LRU-K

实现:底层实现采用两个链表，分别是历史队列和缓存队列。查询时，首先查看缓存队列，若命中，则将访问数据插入到缓存队列的头部。若未命中，则查看历史队列，若命中，则增加该数据的访问次数，若达到k，则将该数据从历史队列移到缓存队列(此时若缓存队列已满，则会淘汰末尾数据)。若扔未命中，则从原始存储中查找数据，然后将数据插入到历史队列的头。

lru_2

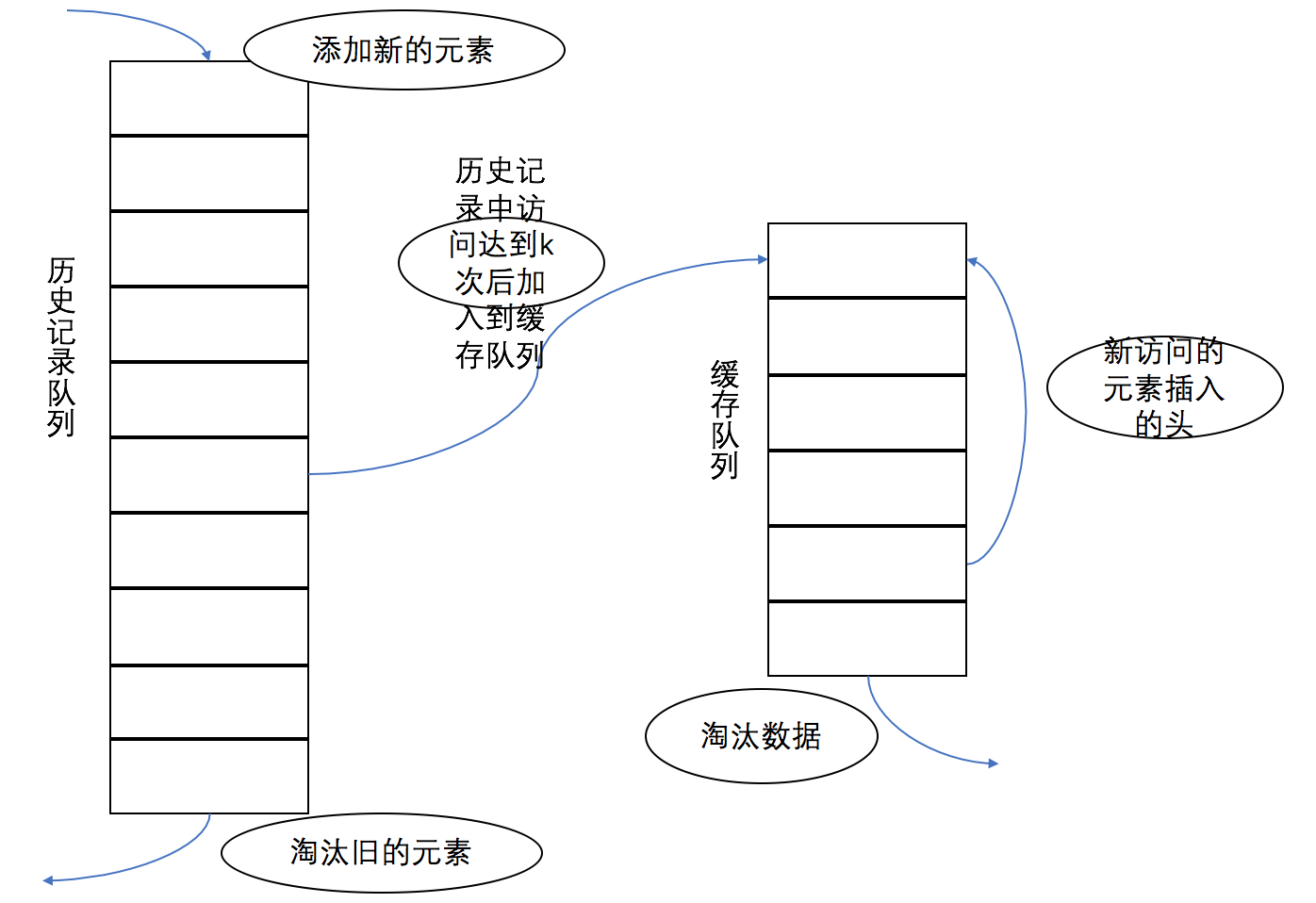
点评:实际使用中，k经常被设置为2。实现较复杂，使用两个队列来实现一个优先级队列。

扩展

LRU-2使用两个队列来实现，一个历史队列，一个缓存队列，其中历史队列是FIFO，缓存队列是LRU。

LRU算法也可以使用多个队列来实现多优先级的队列。

lru_3

展开全文 >>

理论篇-算法总结

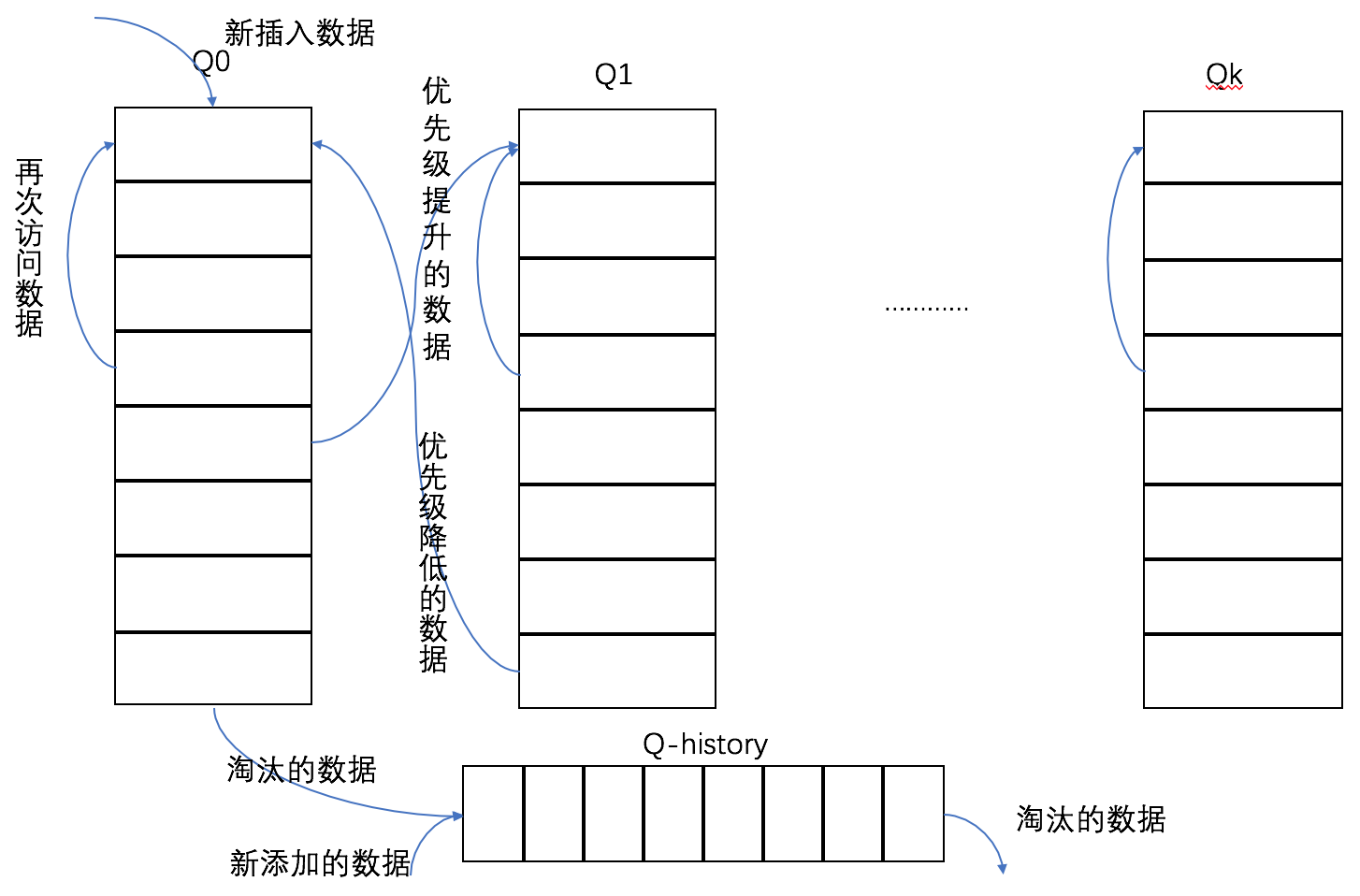
时间负责度被分为两个级别: 多项式级复杂度和非多项式级复杂度

多项式级复杂度: O(1) O(log(n)) O(n^a)

非多项式级复杂度: O(a^n) O(n!)

当我们在解决一个问题的时，我们选择的算法通常都需要是多项式级的复杂度，非多项式级的复杂度计算机往往不能承受，除非数据量非常少。

P问题: 一个可以找到在多项式时间内解决它的算法的问题

NP问题: 可以在多项式时间里验证一个解的问题

NPC问题: 是一类特殊的NP问题。需满足如下两个条件:

  • 它得是一个NP问题
  • 所有的NP问题都可约化到它

NPC问题目前没有多项式的有效算法，只能用指数级甚至阶乘级复杂度的搜索。

题目 时间复杂度
在一个无序序列中寻找最大值或最小值 O(n)
在一个无序序列中寻找任意值 O(n)
在一个无需序列中寻找第k大的值 O(n)
在一个有序序列中寻找最大值或最小值 O(1)
在一个有序序列中寻找任意值 O(lgn)
在一个有序序列中寻找第k大的值 O(1)
在两个有序序列中寻找第k大的值 O(lg(m+n))

经典算法

RSA

reference

什么是P问题、NP问题和NPC问题

展开全文 >>

理论篇-python之元类

元类在class语句执行完之后自动执行。

元类的主要工作: 通过声明一个元类，我们告诉python路由类对象的创建到我们提供的另一个类。

有人使用元类实现面向切面编程和ORM？

元类模型

类是type的实例。
  • 在3.x里，用户定义的类对象是type对象的实例，type对象自身也是一个类
  • 在2.6里，新式类继承自object，object是type的子类。传统类是type的实例，但是不是从类中创建出来的。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
>>> class C: pass           # 2.6中的传统类
...
>>> c = C()
>>> type(c)
<type 'instance'>
>>> type(C)
<type 'classobj'>
>>>
>>> class C(object): pass   # 2.6中的新式类
...
>>> c = C()
>>> type(c)
<class '__main__.C'>
>>> type(C)
<type 'type'>
>>> class C(object): pass   # 3.x中的类
...
>>> c = C()
>>> type(c)
<class '__main__.C'>
>>> type(C)
<class 'type'>
元类是type的子类

元类是type的子类，类是type的实例，所以我们可以通过定制化元类来定制化类。

class声明协议

class声明协议: 在class语句执行完之后，在执行完所有内嵌代码后，会调用type对象来创建class对象。

1
class = type(classname, superclasses, attributedict)

type对象定义了一个__call__方法，该方法运行两个其他的方法。

1
2
type.__new__(typeclass, classname, superclasses, attributedict)
type.__init__(class, classname, superclasses, attributedict)

__new__方法创建和返回新的class对象。__init__初始化新创建的class对象。

举个例子:

1
2
3
4
5
6
class Spam(Eggs):
    data = 1
    def meth(self, arg):
        pass
        
Spam = type('Spam', (Eggs,), {'data': 1, 'meth': meth, '__module__': '__main__'})

声明元类

1
2
3
4
5
6
7
8
9
10
class Spam(Eggs, metaclass=Meta): pass   # 3.0及后续版本
class Spam(object):                      # 2.6 版本
    __metaclass__ = Meta
    
Spam = Meta(classname, superclasses, attributedict)
#后续调用以下方法:
Meta.__new__(class, classname, superclasses, attributedict)
Meta.__init__(Meta, classname, superclasses, attributedict)

python中的高级功能

自省属性: __class__ __dict__

运算符重载方法: __str__ __add__等

属性拦截方法: __getattr__ __setattr__ __getattribute__

类property和类descriptor

函数和类装饰器

元类

展开全文 >>

理论篇-python中好玩的问题

  1. python为什么不支持函数重载？

    其他语言里的函数重载，需要相同的函数名加不同的参数(要么参数的数量不同，要么参数的类型不同)。但是在python里参数是不区分类型的，所以根据类型不同是行不通了。如果在同一个模块里有两个函数名相同，参数数量不同的函数，最后一个函数会覆盖前一个函数。因为函数的定义本质是创建一个函数对象，然后赋值给一个变量名。

  2. python里类的私有变量？

    python中类的私有变量有两种形式: _x和__x。单下划线开头的是一种不正式的约定，双下划线开头的会有一个重命名操作: _class__x。python设计该功能的主要目的是为了防止命名冲突，而不是为了控制访问。

  3. python中有几种可调用的对象?

    四种: 简单函数(def 或 lambda)，继承__call__的实例，绑定方法

展开全文 >>

理论篇-不容易写对的二分查找

前面我们介绍了那么多的排序算法，那对数据排序有什么用呢？这篇文章介绍一个专门针对有序序列的效率极高的查找算法: 二分查找。

核心思想: 首先，找到中间元素，将整个序列分为三部分: 小于等于中间元素的子序列+中间元素+大于等于中间元素的子序列。如果中间元素不是要查找的元素，则根据查找元素与中间元素的关系来决定是在哪个子序列中查找。直到找到或子序列不能分为止。

1
2
3
4
5
6
7
8
9
10
11
12
13
int
binary_search(int *a, int start, int end, int x) {
    int mid;
    
    while (start <= end) {
        mid = (start+end)/2;
        if (a[mid] == x) return mid;
        if (a[mid] > x) end = mid - 1;
        if (a[mid] < x) start = mid + 1;
    }
    
    return -1;
}

备注: 循环截止的条件必须是小于等于，假设数组只有一个元素，此时必须进入循环，判断该元素是不是要查找的值。

展开全文 >>

tag:

    缺失模块。
    1、在博客根目录（注意不是yilia根目录）执行以下命令：
    npm i hexo-generator-json-content --save

    2、在根目录_config.yml里添加配置： 

      jsonContent:
    meta: false
    pages: false
    posts:
      title: true
      date: true
      path: true
      text: true
      raw: false
      content: false
      slug: false
      updated: false
      comments: false
      link: false
      permalink: false
      excerpt: false
      categories: false
      tags: true

王彪<br>计算机科学与技术专业<br>email:841824090@qq.com<br>2009-2013 苏州大学<br>2013-2015 苏州思必驰信息科技有限公司<br>2016-2017 美团<br>2017-至今 搜狗